Все мы привыкли к двоичному коду. Фильмы, игры, картинки, практически вся информация, хранящаяся на наших устройствах и даже искусственный интеллект, все представлены в виде битов, двоичных единицах, которые могут быть либо единицей, либо нулём. Но почему именно два значения? Можем ли мы добавить больше?
На самом деле, да. Добавив третье значение, мы получим троичную систему и превратим биты в триты. То есть каждая единица информации будет принимать одно из уже трёх значений: ноль, единица или двойка. Повлияет ли это на эффективность наших компьютеров? Да, повлияет.
https://youtu.be/NIq0dOAJZ-Y
Троичная логика сильно увеличит объем информации, с которой может работать процессор, то есть повысит диапазон чисел. Помимо этого, также улучшится эффективность процессора из-за уменьшения количества бесполезных операций и логических элементов.
Но почему мы до сих пор сидим на двоичных вычислениях? Где применяется троичная логика? Как она прокачала Базы данных? И при чем тут квантовые компьютеры?
Основная Часть
Вспомним двоичную логику. Перед разбором троичной логики, давайте вспомним как работает её младшая — двоичная версия. Двоичная логика состоит из логических операторов. По сути, это функция, которая принимает один или два входящих логических сигнала и выводит результат. Комбинация этих операторов (их еще называют вентили) и логических сигналов дает логическое выражение.
Например, возьмём выражение с двумя значениями A и B. И A, и B могут принимать значения 0 или 1, True или False. Теперь, чтобы получить решение нашего выражения, нам нужен правильный вентиль.
Есть три базовых оператора: NOT, AND и OR.
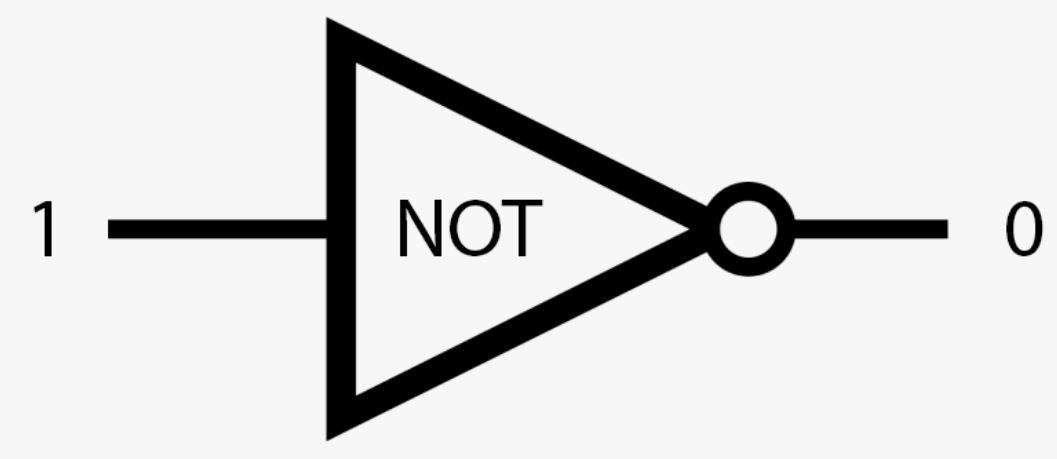
NOT инвертирует значение на противоположное, то есть NOT 1 — это 0, и наоборот.
Вентиль AND работает следующим образом. Допустим, у нас на столе стоит много кружек с водой. Каждая кружка либо наполнена, либо пуста. Полная кружка это 1, пустая — 0. Если поставить между кружками вентили AND, то финальным ответом выражения будет 1, если все кружки окажутся наполненными, и 0, если хотя бы одна пуста.
AND, по сути, берет минимальное среди имеющихся значений. Если хотя бы одно значение равно 0, то ответ 0, если нет, то ответ — 1. Как правило, найдя хотя бы один ноль, мы может игнорировать остальную часть выражения, так как результат всё равно будет ноль.
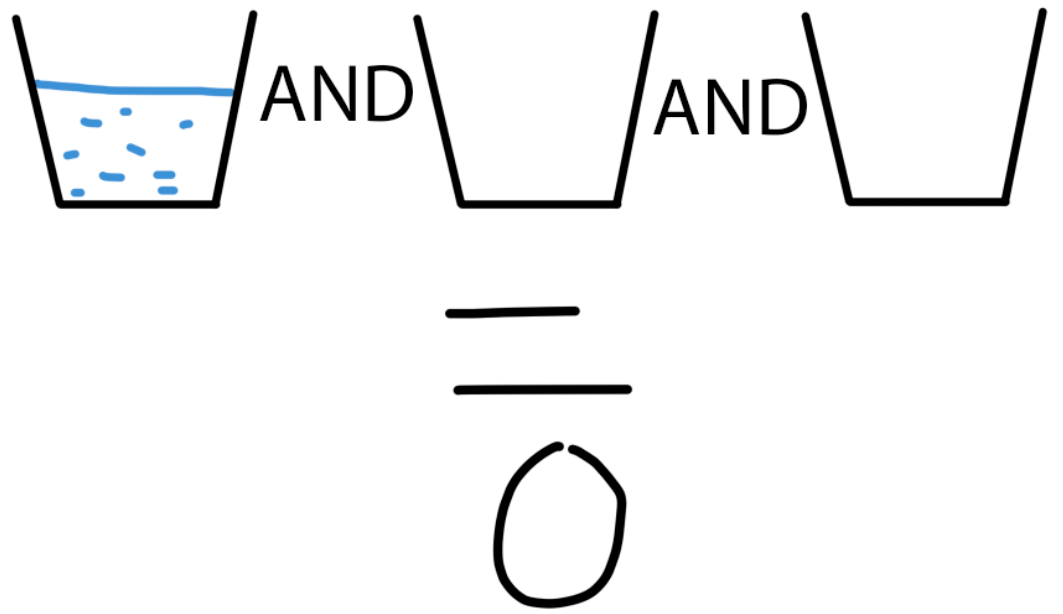
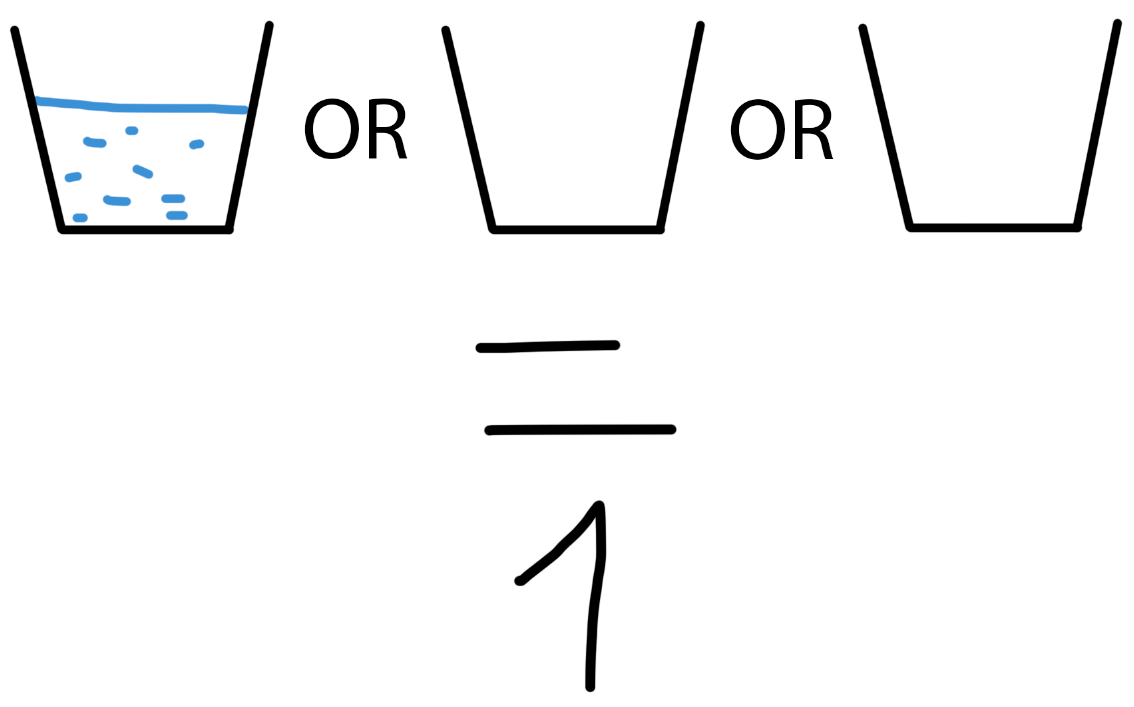
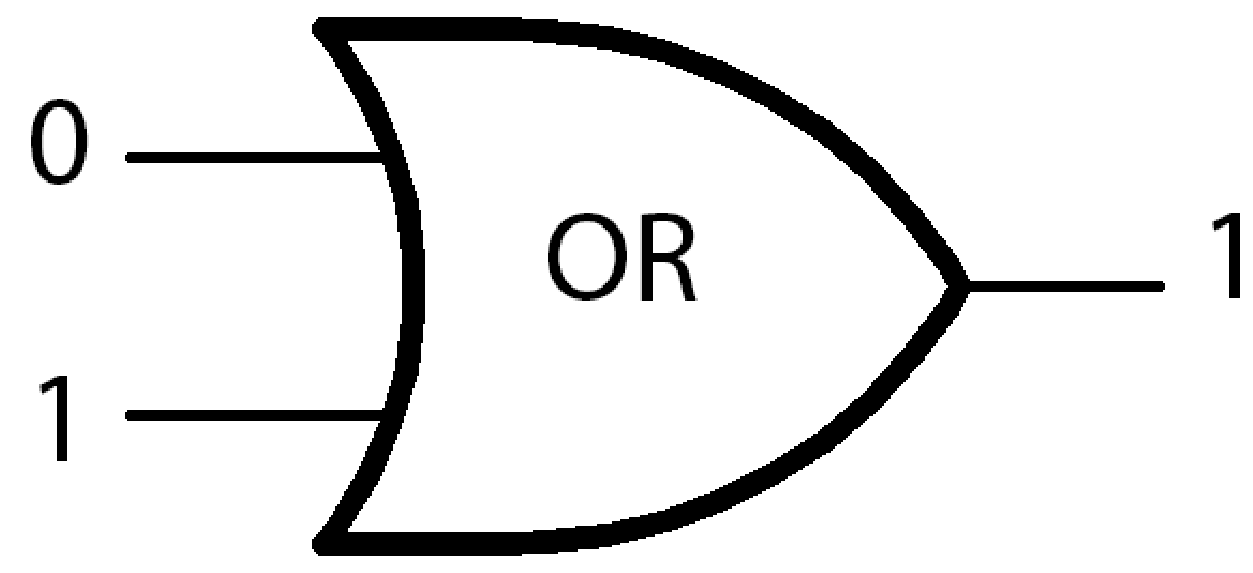
Если AND — это минимальное значение, то OR — максимальное. Возьмём наше выражение с кружками, но заменим все вентили AND на OR. Теперь только одна полная кружка уже даст ответ 1. Если хотя бы одно значение это 1, то результат 1, в другом случае результат 0. То есть мы всегда берём максимальное значение.
Вернемся к нашим значениям A и B. Допустим, A это 1, а B это 0. В данном случае наши вентили будут выглядеть следующим образом.

Теперь, когда мы вспомнили принцип работы двоичной логики, давайте взглянем на троичную. Чем она отличается? И главное — зачем вообще биту третье значение?
Начнём с истоков. Автор первой троичной логики — польский философ Ян Лукасевич, описавший троичную логику в 1920-м году. Лукасевича смотивировала проблема морского боя Аристотеля. Работает она следующим образом. Возьмём фразу: “Через год Apple выпустит умный холодильник” Что можно сказать об этом утверждении?
Оно не является правдой и не является ложью, так как мы просто можем не знать, что произойдет через год. Соответственно, имея только два варианта ответа — истина и ложь — мы не сможем дать правильный ответ. Чтобы разобратся с этим, Лукасевич решил ввести третье значение в двоичную логику — неизвестно, означающее, что в данный момент времени, мы не можем дать точный ответ на вопрос. Но как же третье значение работает с True и False? Сейчас объясним.
Принцип работы троичной логики Клини
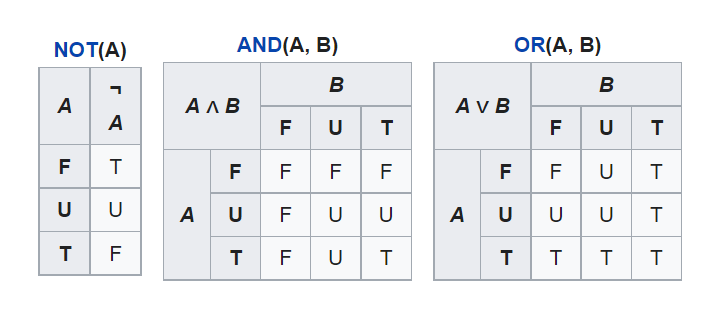
В троичной логике дополнительное значение является либо True, либо False, но в данный момент выяснить, чем именно невозможно, поэтому оно обозначено U, то есть Unknown.
Возьмём за пример выражение “Я ем дошик и Через год Apple выпустит умный холодильник”. Разберем это выражение по логическим частям. Возьмем первую. Допустим я действительно ем дошик. Это значит, что первая часть предложения “я ем дошик” — истина. Теперь посмотрим на вторую часть “через год Apple выпустит умный холодильник”. Мы не знаем, что это True или false. Поэтому его значение Unknown. Поскольку значение второй части напрямую влияет на результат всего выражения, а ответ мы не знаем, мы не можем дать конечный ответ, истина это или ложь, соответственно значение ВСЕГО выражения: “не знаю” или же Unknown.
Я ем дошик = True. Через год Apple выпустит умный холодильник = Unknown
Я ем дошик И Через год Apple выпустит умный холодильник. True AND Unknown = Unknown
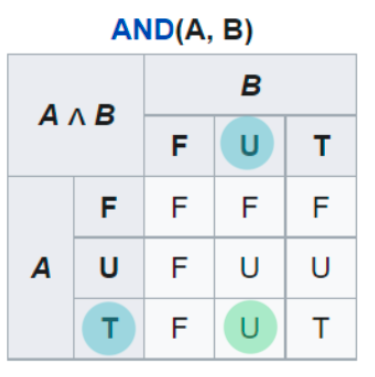
Теперь, мы немного изменим наше выражение. “Я ем дошик ИЛИ Через год Apple выпустит умный холодильник”. В этом случае, мы берем максимальное значение — решение первой части предложения “Правда” или же 1. Это значит, что ответ на вторую, неизвестную часть предложения никак не влияет на конечный результат, так как мы уже нашли максимум, соответственно ответ, в данном случае, истина.
Я ем дошик ИЛИ Через год Apple выпустит умный холодильник. True OR Unknown = True
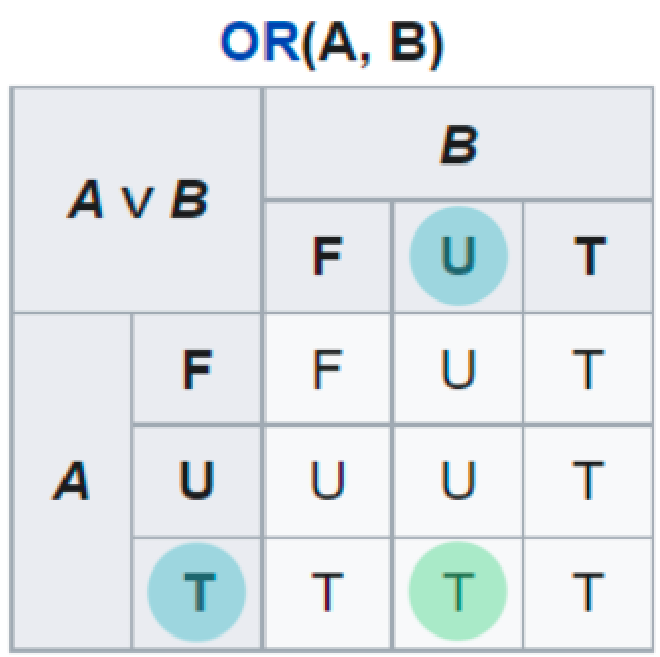
Эта логика называется “Сильная логика Клини”, в честь американского математика Стивена Коула Клини. Она позволяет избежать ответа на сложный вопрос в данный момент времени. Это третье значение часто используется в базах данных дабы указать на отсутствие информации.
Парадокс лжеца
Логика Клини не решает сложные задачи, она избегает ответ. Теперь мы рассмотрим логику, которая способна ответить даже на самые парадоксальные вопросы. Например возьмём проблему с двумя кнопками.
Перед вами две кнопки. Надпись на синей кнопке утверждает, что красная кнопка врёт, а надпись на красной кнопке говорит, что синяя кнопка говорит правду. Вопрос в том, какой кнопке стоит доверять. Не старайтесь, эту задачу мы решить не можем, так как просто не знаем кто лжец. Парадокс в противоречии. Как кнопка может врать и говорить правду одновременно? Нам остаётся только сказать, что ответ неизвестен. Но, есть вариант троичной логики, который способен ответить на этот вопрос. Эта логика называется логика парадокса.

Логика парадокса
Отличие парадоксальной логики в том, как мы определяем значение “истина”. В логике Клини истина это всегда True, в то время как в парадоксальной логике истина это то, что не False. Следите за руками. То есть Unknown в виде результата выражения равняется True.
Самое интересное в этой логике то, что третье значение сразу и True и False. Почему? Сейчас объясним на простом примере. Допустим мы возьмём уже знакомое нам выражение “Через год Apple выпустит умный холодильник” и продублируем его, но инвертируем и добавим вентиль AND между ними. В итоге мы получим выражение: “Через год Apple выпустит умный холодильник И Через год Apple не выпустит умный холодильник”. В обычной логике эта фраза не имеет никакого смысла, но не в логике парадокса.
Как уже упоминалось ранее, мы не знаем ответ на это выражение, значит результат — Unknown, и по правилам троичной логики, противоположность неизвестного значения — неизвестно. В упрощённом варианте это выражение выглядит так (UNKNOWN AND NOT UNKNOWN). Что всё это значит?
И идея в том, что мы не можем сказать, что это утверждение однозначно ложное.
А значит, считает логика парадокса, его можно считать истинным.
Отсюда и парадокс. Как Apple выпустит умный холодильник и не Apple выпустит умный холодильник одновременно?
- A = Через год Apple выпустит умный холодильник
- NOT A = Через год Apple не выпустит умный холодильник
- Через год Apple выпустит умный холодильник И Через год Apple не выпустит умный холодильник
- A AND NOT A
Как улучшить компьютер?
Теперь о применении. Троичная логика в компах сильно увеличит объем информации, с которой может работать процессор. Смотрите, возьмём 1 мегабайт в двоичной системе или же 1,048,576 байт, ну или сразу 8,388,608 бит. Ровно столько клеток имеет процессор для хранения информации. Всего такой комп может хранить 2^8,388,608 разных чисел.
Теперь представим, что компьютер стал троичным. Каждая клетка уже хранит одно из трех значений. Соответственно, количество возможных чисел возрастает до 3^8,388,608. Сколько же это в битах? Для того, чтобы это выяснить, нам нужно найти логарифм этого числа в третьей степени (не уверен так ли правильно сказать) (log 3^8,388,608). Финальное значение 13,295,629 бит. Прирост примерно 58% из-за того, что число 3 ближе к числу e, равному 2.71828. При этом приросте мы не увеличиваем количество клеток в памяти, что просто офигенно.
Что касается скорости, с приходом троичных компов, сильно возрастает эффективность процессоров, так как количество бесполезных операций заметно упадет. Это означает, что на выполнение задач троичный комп требует меньше логических элементов, чем двоичный. Например, для определения знака числа, троичный комп произведет всего одну операцию, а двоичному нужно две.
Меньшее количество элементов, в свою очередь, ускоряет обработку информации, повышает надёжность, сокращает энергопотребление и тепловыделение, а также снижает стоимость. Ваши смартфоны стали бы легче, быстрее, холоднее и дешевле.
Заключение
Где применяется? Так, с троичной логикой разобрались, теперь перейдем к тому, где она применяется.
Троичный компьютер. Самым первым троичным компом был «Сетунь», созданный в 1958-ом году нашими соотечественниками из МГУ.

Невероятно эффективная машина, которая показывала примерно 95% полезного времени в операциях. Другими словами «Сетунь» почти не тратил времени на бесполезные задачи по типу операции на определение знака числа. К слову, в те времена другие компы в лучшем случае имели только 60% полезного времени.
Произвели на свет всего 50 штук, но к сожалению запустить «Сетунь» в массовое производство не удалось. Правительство СССР было против этой технологии и в 1965-ом производство свернули, заменив на двоичные аналоги.
Интересно то, что, чтобы приблизить двоичный компьютер по эффективности к «Сетунь», потребовалось потратить в 2,5 больше денег из-за тех же лишних операций.
База данных
Базы данных на основе языка SQL также используют троичнную логику. Значение null в SQL означает отсутствие информации и может являться чем угодно. Если это значение влияет на финальное выражение, то результат будет неизвестен, или же Unknown. Всё, как в логике Клини.
К примеру, нам нужно получить имя и фамилию пользователя. Если мы знаем имя, но не знаем фамилию, мы можем просто заменить ответ на null, то есть неизвестное значение.
Квантовый компьютер (в будущем)
Теперь поговорим про квантовые компьютеры. В одном из наших прошлых роликов мы рассказывали про принцип работы кубитов. В кратце, квантовые биты способны принимать сразу два значения, единица и ноль одновременно. Это состояние называется суперпозицией.
Но что будет если мы и здесь всунем триты? В итоге мы получим кутриты, которые способны находится в суперпозиции уже не с двумя значениями одновременно, а тремя.
Преимущество кутритов над кубитами, по сути, то же, что и тритов над битами. Кутриты могут существенно упростить реализацию некоторых квантовых алгоритмов и компьютеров, тем самым увеличить эффективность, а также эффективность памяти.
Почему не прижилась?
Теперь перейдем к тому, почему мы до сих пор не используем троичную логику в наших компьютерах. Эксперименты с повседневными троичными компьютерами несомненно проводились и удачно, но в итоге попытки их распространения провалились, так как все всё равно остались сидеть на двоичных.
Причина достаточно банальна. Мы слишком привыкли к битам и переход на троичную логику бы значил переработку вообще всего, начиная с языков программирования, заканчивая строением процессоров, что потребовало бы огромных вложений как и времени, так и денег.
Ещё одна причина заключается в принципе работы транзисторов в процессоре. Напряжение в них колеблется, поэтому добавив дополнительные значения, сигнал может менять состояния когда не нужно. А также троичная система счисления просто пока не нужна. На данный момент той эффективности, которую нам дают два значения нам вполне хватает.